Irving Fisher was not the first to suspect the presence of chaos in the "business cycle". In 1900 a Frenchman named Louis Bachelier proposed that fluctuations in prices of stocks and shares, and thus the underlying structure of the market economy, are effectively random. Bachelier's name does not tend to features in economics textbooks, for he was not an economist. He was a physicist, studying for his doctorate at the École Normale Supérieure under the eminent mathematical physicist Henri Poincaré, whose work supplied the foundations of modern chaos theory. bachelier's thesis was unusual: it economics based on ideas from physics. For his contemporaries this was simply too strange, and Bachelier made no subsequent impact either on science or on economics.
Yet what Bachelier achieved in his thesis was remarkable. To construct a mathematical description of random fluctuations, he had to devise what amounted to a theory of the random walk problem - five years before Einstein began to secure fame with his own treatment of the matter in his celebrated study of Brownian motion. The direction of motion of a particle undergoing a random walk fluctuates unpredictably, and Bachelier assumed that stock prices do the same. The fluctuations are kind of noise. We saw in Chapter 2 how this background of random "static" due to erratic particle motions pervades everything, and that its amplitude is a measure of temperature. The hotter a gas is, the more pronounced are the fluctuations of its constituent particles. In other words, there is a characteristic scale to the fluctuations of particles undergoing random walks - a typical size of deviations.
A random walk has a very well-defined mathematical signature which emerges from the statics of the process. It is impossible to say, at any instant, how big the next random change in direction will be. But if we keep a tally of the size of these fluctuations over a sufficient time span, a pattern becomes clear. let's say we draw a graph of the size of the fluctuations against the number of times such fluctuations appear. What we find is our familiar bell-shaped curve: De Moivre's error curve, championed by Adolphe Quetelet as the hidden regularity of social statistics, and now generally know as Gaussian curve. As the statisticians of the nineteenth century discovered, any set of quantities whose values are randomly determined will fit onto a curve like this.
Source: Critical Mass - how one thing leads to another - by Philip Ball
Example – The S&P 500
Please to check the whole material click on the link below.
http://homepage.mac.com/j.norstad/finance/ranwalk.pdf
Abstract
We develop the formal mathematics of the lognormal random walk model. We
start by discussing continuous compounding for risk-free investments. We introduce
a random variable to model the uncertainty of a risky investment. We
apply the Central Limit Theorem to argue that under three strong assumptions,
the values of risky investments at any time horizon are lognormally distributed.
We model the random walk using a stochastic differential equation. We define
the notion of an “Ito process” and prove that it is equivalent to our formulation.
We apply the model to the S&P 500 stock market index as an example. We
learn how to do parameter estimation for the model using historical time series
data and how to do calculations in the model in computer programs. We discuss
how uncertainty and risk increase with time horizon when investing in volatile
assets like stocks, contrary to popular opinion.
We conclude by asking the all-important question of how well the simple random
walk model describes how financial markets actually work. We mention known
failings of the model and conclude that at best it is a rough approximation to
reality and should be used for real-life financial planning with caution.
We assume that the reader is familiar with the normal and lognormal probability
distributions as presented in reference [8].
Price trends on speculative markets: Trends or Random Walks?
To check this article please click on the link below.
Stock Market Prices Do Not Follow Random Walks :Evidence from a Simple Specification Test
SINCE KEYNES' (1936) NOW FAMOUS PRONOUNCEMENT that most investors'
decisions "can only be taken as a result of animal spirits-of a spontaneous
urge to action rather than inaction, and not as the outcome of a weighted
average of benefits multiplied by quantitative probabilities," a great deal
of research has been devoted to examining the efficiency of stock market
price formation . In Fama's (1970) survey, the vast majority of those studies
were unable to reject the "efficient markets" hypothesis for common stocks .
Although several seemingly anomalous departures from market efficiency
have been well documented, I many financial economists would agree with
Jensen's (1978a) belief that "there is no other proposition in economics
which has more solid empirical evidence supporting it than the Efficient
Markets Hypothesis ."
note to continuous reading this article please click on the link below:
Random walk
Source:
From Wikipedia, the free encyclopedia
Various different types of random walks are of interest. Often, random walks are assumed to be
Markov chains or
Markov processes, but other, more complicated walks are also of interest. Some random walks are on
graphs, others on the line, in the plane, or in higher dimensions, while some random walks are on
groups. Random walks also vary with regard to the time parameter. Often, the walk is in discrete time, and indexed by the natural numbers, as in

. However, some walks take their steps at random times, and in that case the position
Xt is defined for the continuum of times
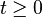
. Specific cases or limits of random walks include the
drunkard's walk and
Lévy flight. Random walks are related to the
diffusion models and are a fundamental topic in discussions of
Markov processes. Several properties of random walks, including dispersal distributions, first-passage times and encounter rates, have been extensively studied.
Lattice random walk
A popular random walk model is that of a random walk on a regular lattice, where at each step the walk jumps to another site according to some probability distribution. In
simple random walk, the walk can only jump to neighbouring sites of the lattice. In
simple symmetric random walk on a locally finite lattice, the probabilities of walk jumping to any one of its neighbours are the same. The most well-studied example is of random walk on the d-dimensional integer lattice (sometimes called the hypercubic lattice)

.
[edit]One-dimensional random walk
Imagine a one-dimensional length of something, a '
line'. Now imagine this line has numbers on it, spaced apart equally. A particularly elementary and concrete random walk is the random walk on the
integer number line,

, which starts at

and at each step moves by ±1 with equal probability. To define this walk formally, take independent random variables
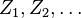
, where each variable is either 1 or −1, with a 50% probability for either value, and set
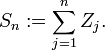
The
series 
is called the
simple random walk on 
. This series (the sum of the sequence of -1's and 1's) gives you the length you have 'walked', if each part of the walk is of length one.
This walk can be illustrated as follows. Say you flip a fair coin. If it lands on heads, you move one to the right on the number line. If it lands on tails, you move one to the left. So after five flips, you have the possibility of landing on 1, −1, 3, −3, 5, or −5. You can land on 1 by flipping three heads and two tails in any order. There are 10 possible ways of landing on 1. Similarly, there are 10 ways of landing on −1 (by flipping three tails and two heads), 5 ways of landing on 3 (by flipping four heads and one tail), 5 ways of landing on −3 (by flipping four tails and one head), 1 way of landing on 5 (by flipping five heads), and 1 way of landing on −5 (by flipping five tails). See the figure below for an illustration of this example.

What can we say about the position

of the walk after
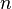
steps? Of course, it is random, so we cannot calculate it. But we may say quite a bit about its distribution. It is not hard to see that the
expectation 
of

is zero. That is, the more you flip the coin, the closer the mean of all your -1's and 1's will be to zero. For example, this follows by the finite additivity property of expectation:
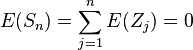
. A similar calculation, using the independence of the random variables

, shows that

. This hints that

, the
expected translation distance after
n steps, should be
of the order of 
. In fact,

Suppose we draw a line some distance from the origin of the walk. How many times will the random walk cross the line if permitted to continue walking forever? The following, perhaps surprising theorem is the answer: simple random walk on

will cross every point an infinite number of times. This result has many names: the
level-crossing phenomenon,
recurrence or the
gambler's ruin. The reason for the last name is as follows: if you are a gambler with a finite amount of money playing
a fair game against a bank with an infinite amount of money, you will surely lose. The amount of money you have will perform a random walk, and it will
almost surely, at some time, reach 0 and the game will be over.
If
a and
b are positive integers, then the expected number of steps until a one-dimensional simple random walk starting at 0 first hits
b or −
a is
ab. The probability that this walk will hit
b before
-a steps is
a / (a + b), which can be derived from the fact that simple random walk is a
martingale.
Some of the results mentioned above can be derived from properties of
Pascal's triangle. The number of different walks of
n steps where each step is +1 or −1 is clearly 2
n. For the simple random walk, each of these walks are equally likely. In order for
Sn to be equal to a number
k it is necessary and sufficient that the number of +1 in the walk exceeds those of −1 by
k. Thus, the number of walks which satisfy
Sn = k is precisely the number of ways of choosing (
n +
k)/2 elements from an
n element set (for this to be non-zero, it is necessary that
n +
k be an even number), which is an entry in Pascal's triangle denoted by
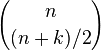
. Therefore, the probability that
Sn = k is equal to

. By representing entries of Pascal's triangle in terms of
factorials and using
Stirling's formula, one can obtain good estimates for these probabilities for large values of
n.
This relation with Pascal's triangle is easily demonstrated for small values of n. At zero turns, the only possibility will be to remain at zero. However, at one turn, you can move either to the left or the right of zero, meaning there is one chance of landing on −1 or one chance of landing on 1. At two turns, you examine the turns from before. If you had been at 1, you could move to 2 or back to zero. If you had been at −1, you could move to −2 or back to zero. So there is one chance of landing on −2, two chances of landing on zero, and one chance of landing on 2.
| n | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|
| P[S0 = k] | | | | | | 1 | | | | | |
| 2P[S1 = k] | | | | | 1 | | 1 | | | | |
| 22P[S2 = k] | | | | 1 | | 2 | | 1 | | | |
| 23P[S3 = k] | | | 1 | | 3 | | 3 | | 1 | | |
| 24P[S4 = k] | | 1 | | 4 | | 6 | | 4 | | 1 | |
| 25P[S5 = k] | 1 | | 5 | | 10 | | 10 | | 5 | | 1 |
[edit]Gaussian random walk
A random walk having a step size that varies according to a
normal distribution is used as a model for real-world time series data such as financial markets. The
Black-Scholes formula for modeling option prices, for example, uses a gaussian random walk as an underlying assumption.
Here, the step size is the inverse cumulative normal distribution Φ − 1(z,μ,σ) where 0 ≤ z ≤ 1 is a uniformly distributed random number, and μ and σ are the mean and standard deviations of the normal distribution, respectively.
For steps distributed according to any distribution with zero mean and a finite variance (not necessarily just a normal distribution), the root mean squared translation distance after n steps is






 . However, some walks take their steps at random times, and in that case the position
. However, some walks take their steps at random times, and in that case the position  . Specific cases or limits of random walks include the drunkard's walk and
. Specific cases or limits of random walks include the drunkard's walk and  .
. , which starts at
, which starts at  and at each step moves by ±1 with equal probability. To define this walk formally, take independent random variables
and at each step moves by ±1 with equal probability. To define this walk formally, take independent random variables  , where each variable is either 1 or −1, with a 50% probability for either value, and set
, where each variable is either 1 or −1, with a 50% probability for either value, and set 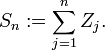 The
The  is called the simple random walk on
is called the simple random walk on  of the walk after
of the walk after 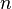 steps? Of course, it is random, so we cannot calculate it. But we may say quite a bit about its distribution. It is not hard to see that the
steps? Of course, it is random, so we cannot calculate it. But we may say quite a bit about its distribution. It is not hard to see that the of
of 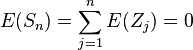 . A similar calculation, using the independence of the random variables
. A similar calculation, using the independence of the random variables  , shows that
, shows that  . This hints that
. This hints that  , the
, the  . In fact,
. In fact,
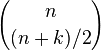 . Therefore, the probability that
. Therefore, the probability that  . By representing entries of Pascal's triangle in terms of
. By representing entries of Pascal's triangle in terms of 